|
仧 p,19 仧 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
|---|
|
亂鶮b丒嘍亃
丂丂傑偨丄偙偺乭柦戣偺堦斒揑宍幃乭偲偄偆傕偺傪丄峫偊傞偙偲偵傛偭偰乽悢乿偲偄偆傕偺偲柦戣偺娭學偑丄丂丂丂丂丂 丂丂柧妋側偐偨偪偱昞尰偱偒傞偲偄偆偙偲偵傕側傞丅偡側傢偪丄偦傟偼丂乭憖嶌乭偲偄偆偙偲偵傛偭偰娭學 丂丂傪帩偭偰偄傞偺偱偁傞丅乮傕偟偔偼丄偦傟偩偗偺偮側偑傝偲傕偄偊傞偙偲偲側傞丅乯 丂丂柦戣偺堦斒揑宍幃傪丄憖嶌丂偲偄偆娤揰偱丂昞尰偟捈偟偨応崌丄梫慺柦戣偺偁傞揔摉側廤崌偺昞尰丂 |
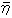 丂丂傪梡偄傞偲丄偁傞柦戣孮偑偁傝偦傟偵崻杮憖嶌俶傪傎偳偙偟丄懕偄偰暿偺柦戣孮偺偵傛傞傕偺傕弌棃偰
丂丂偄偔乭堏峴乭偺堦斒揑側奿岲偵偍偄偰丄
丂丂傪梡偄傞偲丄偁傞柦戣孮偑偁傝偦傟偵崻杮憖嶌俶傪傎偳偙偟丄懕偄偰暿偺柦戣孮偺偵傛傞傕偺傕弌棃偰
丂丂偄偔乭堏峴乭偺堦斒揑側奿岲偵偍偄偰丄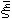 丄
丄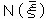 乴丄乮
乴丄乮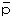 偺戙傢傝偵巒傔偱側偔偰傕偄偄偲偡傞偲
偺戙傢傝偵巒傔偱側偔偰傕偄偄偲偡傞偲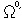 偦偟偰傕偲偺忬懺偱傕偁傞偐傜丄偙傟偼
丂丂亖倃偲傕偄偊傞丅Def侾
丂丂傑偨丄憖嶌傪廳偹傞偙偲傕丂
偦偟偰傕偲偺忬懺偱傕偁傞偐傜丄偙傟偼
丂丂亖倃偲傕偄偊傞丅Def侾
丂丂傑偨丄憖嶌傪廳偹傞偙偲傕丂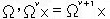 丂偲偟偰丄巜悢偺亄侾偱昞尰偡傞丅Def2
丂丂偦偟偰丄偙偺Def侾偲俀傪婰崋偺掕媊偲偡傞偲丄
丂丂x丄兌乫x丄兌乫兌乫x丄兌乫兌乫兌乫x丄ゥゥ偲偄偆憖嶌傪廳偹偰懕偗偨楍偼巜悢昞尰傪巊偭偰丄
丂丂
丂偲偟偰丄巜悢偺亄侾偱昞尰偡傞丅Def2
丂丂偦偟偰丄偙偺Def侾偲俀傪婰崋偺掕媊偲偡傞偲丄
丂丂x丄兌乫x丄兌乫兌乫x丄兌乫兌乫兌乫x丄ゥゥ偲偄偆憖嶌傪廳偹偰懕偗偨楍偼巜悢昞尰傪巊偭偰丄
丂丂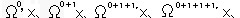 偲彂偒昞偣傞丅
丂丂巜悢偺晹暘偩偗傪尒傟偽丄
丂丂侽丆侽亄侾丄侽亄侾亄侾丄侽亄侾亄侾亄侾偲偄偆傕偺偑柦戣偺堦斒宍幃偐傜丄惉傝棫偨偣傞偙偲偑弌棃偨
丂丂栿偵側傞丅
丂丂偦偟偰丄屄乆偵懳墳偡傞婰崋偲偟偰晛捠偺悢偺婰崋乮侽偲侾埲奜偺傾儔價傾悢帤偺暥帤乯傪掕媊偟偰丄
丂丂侽亄侾亖侾丄侽亄侾亄侾亖俀丄侽亄侾亄侾亄侾亖俁丄奺乆掕媊偟偰etcゥiDef乯
丂丂僂傿僩僎儞僔儏僞僀儞偼丄偙偺傛偆側傗傝曽偱乽悢乿傪偲傜偊傞丅
丂丂傑偨丄弶摍嶼弍偵偮偄偰傕丄壛朄亄偼丄忋偺掕媊偺拞偵傕偆婯掕偝傟偰偄傞偑丄乮尭朄傕偙偙偐傜扨弮偵
丂丂婰崋朄偺岺晇偱弌偰偔傞偩傠偆偐傜乯忔朄亊偺曽偼丄悢妛偵偍偗傞崻杮揑側乭戙擖朄乭丄摍幃偲偄偆庡岅
丂丂乕弎岅娭學側偳偲偼堘偆娭學偵偍偗傞乭抲姺壜擻惈乭偺慡斒壔偐傜乮巐懃側偳傕偱偰偔傞乯丄壛朄偺幃偵
丂丂懳偟妵屖傗戙擖偵傛傞擖傟懼偊傪偝傜偵峫偊傞偲妡偗嶼偺徹柧偑偱偒傞丅偡側傢偪丄
忔朄偲偼丄俀乮a亄a乯亖係a丂偲偄偆傛偆側妵屖撪偺憖嶌偵妵屖奜偺憖嶌偑奺乆巤偝傟傞
丂偙偲偵傛偭偰杮幙乮榑棟偵偍偗傞乯偑帵偝傟傞嶼弍寁嶼側偺偱偁傝丄
丂丂
偲彂偒昞偣傞丅
丂丂巜悢偺晹暘偩偗傪尒傟偽丄
丂丂侽丆侽亄侾丄侽亄侾亄侾丄侽亄侾亄侾亄侾偲偄偆傕偺偑柦戣偺堦斒宍幃偐傜丄惉傝棫偨偣傞偙偲偑弌棃偨
丂丂栿偵側傞丅
丂丂偦偟偰丄屄乆偵懳墳偡傞婰崋偲偟偰晛捠偺悢偺婰崋乮侽偲侾埲奜偺傾儔價傾悢帤偺暥帤乯傪掕媊偟偰丄
丂丂侽亄侾亖侾丄侽亄侾亄侾亖俀丄侽亄侾亄侾亄侾亖俁丄奺乆掕媊偟偰etcゥiDef乯
丂丂僂傿僩僎儞僔儏僞僀儞偼丄偙偺傛偆側傗傝曽偱乽悢乿傪偲傜偊傞丅
丂丂傑偨丄弶摍嶼弍偵偮偄偰傕丄壛朄亄偼丄忋偺掕媊偺拞偵傕偆婯掕偝傟偰偄傞偑丄乮尭朄傕偙偙偐傜扨弮偵
丂丂婰崋朄偺岺晇偱弌偰偔傞偩傠偆偐傜乯忔朄亊偺曽偼丄悢妛偵偍偗傞崻杮揑側乭戙擖朄乭丄摍幃偲偄偆庡岅
丂丂乕弎岅娭學側偳偲偼堘偆娭學偵偍偗傞乭抲姺壜擻惈乭偺慡斒壔偐傜乮巐懃側偳傕偱偰偔傞乯丄壛朄偺幃偵
丂丂懳偟妵屖傗戙擖偵傛傞擖傟懼偊傪偝傜偵峫偊傞偲妡偗嶼偺徹柧偑偱偒傞丅偡側傢偪丄
忔朄偲偼丄俀乮a亄a乯亖係a丂偲偄偆傛偆側妵屖撪偺憖嶌偵妵屖奜偺憖嶌偑奺乆巤偝傟傞
丂偙偲偵傛偭偰杮幙乮榑棟偵偍偗傞乯偑帵偝傟傞嶼弍寁嶼側偺偱偁傝丄
丂丂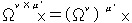 丂偲偝傟丄兯倃兪偲偼妵屖偱妘偰傜傟偨巜悢偺兯兪偺偙偲偲偟偰掕媊偲側傞偺偱丄
丂丂乮傑偨丂埲壓偺幃側偳偵偁傞彫偝偄乽 乫乿偼丄屄乆偺婰崋偑偮側偑偭偰側偄偙偲傪帵偡嬫愗傝婰崋乯
丂丂
丂偲偝傟丄兯倃兪偲偼妵屖偱妘偰傜傟偨巜悢偺兯兪偺偙偲偲偟偰掕媊偲側傞偺偱丄
丂丂乮傑偨丂埲壓偺幃側偳偵偁傞彫偝偄乽 乫乿偼丄屄乆偺婰崋偑偮側偑偭偰側偄偙偲傪帵偡嬫愗傝婰崋乯
丂丂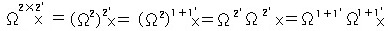 丂丂亖乮兌乫兌乯乫乮兌乫兌乯乫x亖兌乫兌乫兌乫兌乫x亖
丂丂亖乮兌乫兌乯乫乮兌乫兌乯乫x亖兌乫兌乫兌乫兌乫x亖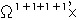 丂亖
丂亖 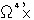 丂丂丂
丂偙偆偄偭偨悢棟榑棟妛摿桳偺婰弎偼摪乆弰傝偺乽掕媊乿偺傛偆偵慺杙偵偼巚傢傟傞傕偺偩偑丄偙傟偑乽掕媊乿
丂偱偁傞偲峫偊傞傛傝丄傑偢敪埬幰偺偙偆偄偭偨栤戣偵懳偡傞丄昞尰朄傪尠傢偟偰偄傞偲峫偊傞曽偑惓偟偄愙
丂嬤偺偟偐偨偵側傞丅幚嵺丄僼儗乕僎傗儔僢僙儖偺悢傗婎杮揑側嶼弍偺掕媊偼丄偄偨偢傜偵偳傫偳傫朿傜傫偱
丂偄偭偨傝偡傞乮僾儕儞僉僺傾側偳偺巚偄偮偒偺傛偆側婰弎偺曄峏偺傛偆側傕偺乯丄偦傟偧傟偺偄偔偮偐偺挊
丂嶌偵尒傞曄峏側偳丄柧傜偐偵壗偐偟傜偺乭摪乆弰傝乭偑暯慠偲峴傢傟偰偄傞寢壥偺報徾偑偁傝丄偦傟偼乭昞
丂尰朄乭偲偟偰廩暘側堄幆偑側偄偺偱側偄偐丠偲偄偆偙偲偱傕偁傞丅
丂偦傟偵斾妑偡傟偽僂傿僩僎儞僔儏僞僀儞偺応崌丄堦尒丂忋偺悢傗忔朄偺愢柧偑丄摪乆弰傝偱側偄偐偲巚偆偺
丂傕丄柦戣傪乽憖嶌乿偡傞偲偄偆偙偲偺娭學偵偍偄偰懆偊傛偆偲堄恾傪峫偊傞側傜丄偙偆偄偭偨堦尒傗傗偙偟
丂偄婰弎傕寢嬊丄悢偼丄崻杮揑偵乽ゥ侾亄侾亄侾亄侾亄ゥ乿偱偁傝丄傑偨乭戙擖朄乭偱偁傞偲偄偆偙偲偱丄柦
丂戣偺傛偆側壗偐偺懳徾傪昤弌偟偨傕偺偱側偔丄偦偺昤幨偟偨柦戣婰崋傪憖嶌偡傞峴堊丄偲偄偆偁傞暿師尦偺
丂孞傝曉偟壜擻側偙偲偺昞尰偱偁傝丄柍棟偺側偄傕偺偲尒偊偰偔傞丅傑偨丄乽屻婜乿偺悢妛婎慴榑偺悢偺掕媊
丂乽悢偊傞乿偲偄偆偙偲傕丄榑棟妛偲偺捈愙揑娭學傪彍偗偽丄憖嶌偡傞峴堊偲偟偰傎偲傫偳摨偠側偺偱偁傞丅
丂亀榑峫亁偵偍偗傞僂傿僩僎儞僔儏僞僀儞偺悢妛榑偑丄僼儗乕僎傗儔僢僙儖側偳偺傛偆偵敊慠偲朿戝壔偣偢丄
丂偦傟偵妑傋傟偽旕忢偵娙扨偵嵪傫偱偟傑偆偺傕丄寛掕揑偵偼乭憖嶌乭傗傑偨丄僂傿僩僎儞僔儏僞僀儞偵偍偄
丂偰嬌傔偰廳梫側敪憐偲側傞乭榑棟揑宍幃乭乮屻弎乯偲偄偆丄偲傕偵丂柦戣偺乭幨憸偟偨傕偺乭乮岅傞乯偲偄
丂偆偺偲崻杮揑偵師尦偺堎側傞傕偺偑偁傞丄偲偄偆峫偊傪帩偰偨偐傜側偺偩丄偲偄偊傞丅
丂偡側傢偪丄悢妛偺懡偔偺晹暘偼榑棟妛偲傓偟傠嫟桳偡傞乽榑棟乿偵傛傞偺偱偁傝丄乭尷傝側偔乭偁傞條乆側
丂榑棟揑宍幃偺娭梌偡傞丄傕偟偔偼偦偺昞尰偱傕偁傞傕偺偲側傞偺偱丄暿偵榑棟妛偱埖偆懳徾偱側偄偙偲偵側
丂傞丅榑棟妛偐傜偼偦偺柦戣偺堦斒揑宍幃偐傜偺乭憖嶌乭側偳偵娭傢傞偙偲偐傜丄捈愙摫偐傟傞嶼弍偺嵟傕婎
丂杮揑側曽朄偵榖戣傪尷傞偙偲偱偁傝丄傓偟傠丄悢妛慡斒偵捈愙娭傢傞偙偲偼丄偦偺嫬奅傪敊慠偲偝偣媝偭偰
丂榑棟揑宍幃側偳偵傑偮傢傞悢棟榑棟妛偺崿棎傪彽偔偙偲偵偮側偑傞丅
丂
丂丂丂
丂偙偆偄偭偨悢棟榑棟妛摿桳偺婰弎偼摪乆弰傝偺乽掕媊乿偺傛偆偵慺杙偵偼巚傢傟傞傕偺偩偑丄偙傟偑乽掕媊乿
丂偱偁傞偲峫偊傞傛傝丄傑偢敪埬幰偺偙偆偄偭偨栤戣偵懳偡傞丄昞尰朄傪尠傢偟偰偄傞偲峫偊傞曽偑惓偟偄愙
丂嬤偺偟偐偨偵側傞丅幚嵺丄僼儗乕僎傗儔僢僙儖偺悢傗婎杮揑側嶼弍偺掕媊偼丄偄偨偢傜偵偳傫偳傫朿傜傫偱
丂偄偭偨傝偡傞乮僾儕儞僉僺傾側偳偺巚偄偮偒偺傛偆側婰弎偺曄峏偺傛偆側傕偺乯丄偦傟偧傟偺偄偔偮偐偺挊
丂嶌偵尒傞曄峏側偳丄柧傜偐偵壗偐偟傜偺乭摪乆弰傝乭偑暯慠偲峴傢傟偰偄傞寢壥偺報徾偑偁傝丄偦傟偼乭昞
丂尰朄乭偲偟偰廩暘側堄幆偑側偄偺偱側偄偐丠偲偄偆偙偲偱傕偁傞丅
丂偦傟偵斾妑偡傟偽僂傿僩僎儞僔儏僞僀儞偺応崌丄堦尒丂忋偺悢傗忔朄偺愢柧偑丄摪乆弰傝偱側偄偐偲巚偆偺
丂傕丄柦戣傪乽憖嶌乿偡傞偲偄偆偙偲偺娭學偵偍偄偰懆偊傛偆偲堄恾傪峫偊傞側傜丄偙偆偄偭偨堦尒傗傗偙偟
丂偄婰弎傕寢嬊丄悢偼丄崻杮揑偵乽ゥ侾亄侾亄侾亄侾亄ゥ乿偱偁傝丄傑偨乭戙擖朄乭偱偁傞偲偄偆偙偲偱丄柦
丂戣偺傛偆側壗偐偺懳徾傪昤弌偟偨傕偺偱側偔丄偦偺昤幨偟偨柦戣婰崋傪憖嶌偡傞峴堊丄偲偄偆偁傞暿師尦偺
丂孞傝曉偟壜擻側偙偲偺昞尰偱偁傝丄柍棟偺側偄傕偺偲尒偊偰偔傞丅傑偨丄乽屻婜乿偺悢妛婎慴榑偺悢偺掕媊
丂乽悢偊傞乿偲偄偆偙偲傕丄榑棟妛偲偺捈愙揑娭學傪彍偗偽丄憖嶌偡傞峴堊偲偟偰傎偲傫偳摨偠側偺偱偁傞丅
丂亀榑峫亁偵偍偗傞僂傿僩僎儞僔儏僞僀儞偺悢妛榑偑丄僼儗乕僎傗儔僢僙儖側偳偺傛偆偵敊慠偲朿戝壔偣偢丄
丂偦傟偵妑傋傟偽旕忢偵娙扨偵嵪傫偱偟傑偆偺傕丄寛掕揑偵偼乭憖嶌乭傗傑偨丄僂傿僩僎儞僔儏僞僀儞偵偍偄
丂偰嬌傔偰廳梫側敪憐偲側傞乭榑棟揑宍幃乭乮屻弎乯偲偄偆丄偲傕偵丂柦戣偺乭幨憸偟偨傕偺乭乮岅傞乯偲偄
丂偆偺偲崻杮揑偵師尦偺堎側傞傕偺偑偁傞丄偲偄偆峫偊傪帩偰偨偐傜側偺偩丄偲偄偊傞丅
丂偡側傢偪丄悢妛偺懡偔偺晹暘偼榑棟妛偲傓偟傠嫟桳偡傞乽榑棟乿偵傛傞偺偱偁傝丄乭尷傝側偔乭偁傞條乆側
丂榑棟揑宍幃偺娭梌偡傞丄傕偟偔偼偦偺昞尰偱傕偁傞傕偺偲側傞偺偱丄暿偵榑棟妛偱埖偆懳徾偱側偄偙偲偵側
丂傞丅榑棟妛偐傜偼偦偺柦戣偺堦斒揑宍幃偐傜偺乭憖嶌乭側偳偵娭傢傞偙偲偐傜丄捈愙摫偐傟傞嶼弍偺嵟傕婎
丂杮揑側曽朄偵榖戣傪尷傞偙偲偱偁傝丄傓偟傠丄悢妛慡斒偵捈愙娭傢傞偙偲偼丄偦偺嫬奅傪敊慠偲偝偣媝偭偰
丂榑棟揑宍幃側偳偵傑偮傢傞悢棟榑棟妛偺崿棎傪彽偔偙偲偵偮側偑傞丅
丂