|
◆ p,18 ◆ |
|---|
|
【Ⅱb・④】
”命題の一般形式”というものを、とらえる際の前提となる考えは、”構造的系列”とウィトゲン シュタインが呼ぶもので、 『 わたしは、構造的系列 ”a、0’a、0’0’a、・・・・・”の一般項を、”〔a、x、0’x〕” と書き表す。括弧で囲まれた表現は、一種の変数である。括弧の中の最初の項は、構造的系 列の初項であり、2番目の項は系列の任意の項xの形式であり、3番目の項はxの直ぐ後に続 く系列の項の形式である。 (TLP 5・2522) 』 ウィトゲンシュタインの系列も、xがyに先立ち、yがzに先立つとき、xはzに先立つ・・・・・と いう、いわゆる移行性の関係のような変化した記号列の一連の一般に多く見られる形と言ってよい が、正し、フレーゲ、ラッセルが自然数列などを定義するときに使った”遺伝的関係”などの発想 に、根本的に批判する立場からこの”系列”という表現は選ばれている。すなわち、ある共通性と 変化を持った記号の連なりは、見る人に何かそれ自体、なにかある対象を表しているような、錯覚 を与えやすいが、それは真理関数などとは根本的に違うのである。こういったものは、”操作”と いわれるもので、ウィトゲンシュタインの”論理的形式”という考え とともに、事象(事実)を 語る命題とはっきり別の次元に置かれることを、強調するのが『論考』の独自な最も中心的な主張 といっていい。すなわち、こういったっものは、初項とある項、そして続く項、というような変数 での表示しかできない。aということがらに、操作”0’ξ”(ξは操作の元となる要素の命題群 を表す)のを3回適用したことは、”0’0’0’a”と書き表される。だから項が3つ以上あれ ば”a、0’a、0’0’a、・・・・・”となる。これはもっと一般的に考えれば命題が、3つ変化した かたち、初項とある項、そして続く項、となる。 それが、 |
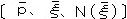 であり、この場合の”操作”が、要素命題をくっつける”否定連言”に
なり、そしてそれだけで済むのである。というのは、シェーファーの棒記号でも結局そうなったよ
うに『プリンキピア・マテマティカ』などで基本的な記号と考えられた「・」「∨」「⊃」などの
個別的記号は、別に不可欠のものでなく消失しうるのである。すなわち、その所属する命題全てを
否定する操作を、「N」という記号を用いて表すと、例えば
否定は、「~p」=「N(p)」、選言(または)は、「p∨q」=「N(N(p、q))」で、
そして、連言(かつ)は、「p・q」=「N(N(p)、N(q))」などとなる。この「N」
を、ウィトゲンシュタインは所詮一種の論理定項のようなシェーファーのようなレベルでなく
命題の真理値で表してしまおうとするのである。すなわち、
『 あらゆる真理命題は、(---W)(ξ、--) という操作を、
諸要素命題に継続的に適用した結果である。 (TLP 5・5) 』
これは、あらゆる命題は、要素命題を複合して出来たもので、その複合の仕方は対応する真理の値
、真偽すなわちWとFとの、関数の形(真理関数)をとる。要素命題は非常に多数となるが、重要
なのは2者の関係となるから、例えばpとqの2つの要素命題がある場合、ξという扱われる要素
命題の素材を表す右の括弧内は、(p、q)で表される。
p、qの2つの場合その真偽の組み合わせは全部で4通りしかなく、その組み合わせの順序を定め
ておくとpとqの作る関係は、その順序に対応した各々の真偽の値が違ったパターンで、固有の順
序を持って表される。すなわち、「p・q」という関係なら、pqの両方とも真である場合しか、
2者の作る関係で真は出来ないので(真偽偽偽)という固有の値を作り、これが左の括弧の中身と
なる。(これらを掛け線の欄で表せばいわゆる”真理表”となる)ウィトゲンシュタインの写像理
論によれば、偽は事実と対応がないということを示すので、空欄のーで表すと(W---)となる。
また「p⊃q」も数理論理学では結果的に包含関係というより真理関係のみで理解されるようなも
のであったから、その真偽値のパターンの一つとして、(--W-)となり、また 同語反復命題、
トートロジーはどの場合も真になるので(WWWW)、逆に矛盾命題はどんな場合も偽となるので、
(----)となる。だから、所属する命題全てを否定する「N」は、(FFFW)もしくは(---W)
のパターンで表されるし、ξとなる要素命題が増えても、この全部否定する場合の真理値のパター
ンは必ず最後だけWとなる値を示すので、Nは一般に(---W)となる。
だから、
『 命題を項に持つ、括弧にくくられた表現ー括弧の中の各項の順序は問わないーを、私は
‘(
であり、この場合の”操作”が、要素命題をくっつける”否定連言”に
なり、そしてそれだけで済むのである。というのは、シェーファーの棒記号でも結局そうなったよ
うに『プリンキピア・マテマティカ』などで基本的な記号と考えられた「・」「∨」「⊃」などの
個別的記号は、別に不可欠のものでなく消失しうるのである。すなわち、その所属する命題全てを
否定する操作を、「N」という記号を用いて表すと、例えば
否定は、「~p」=「N(p)」、選言(または)は、「p∨q」=「N(N(p、q))」で、
そして、連言(かつ)は、「p・q」=「N(N(p)、N(q))」などとなる。この「N」
を、ウィトゲンシュタインは所詮一種の論理定項のようなシェーファーのようなレベルでなく
命題の真理値で表してしまおうとするのである。すなわち、
『 あらゆる真理命題は、(---W)(ξ、--) という操作を、
諸要素命題に継続的に適用した結果である。 (TLP 5・5) 』
これは、あらゆる命題は、要素命題を複合して出来たもので、その複合の仕方は対応する真理の値
、真偽すなわちWとFとの、関数の形(真理関数)をとる。要素命題は非常に多数となるが、重要
なのは2者の関係となるから、例えばpとqの2つの要素命題がある場合、ξという扱われる要素
命題の素材を表す右の括弧内は、(p、q)で表される。
p、qの2つの場合その真偽の組み合わせは全部で4通りしかなく、その組み合わせの順序を定め
ておくとpとqの作る関係は、その順序に対応した各々の真偽の値が違ったパターンで、固有の順
序を持って表される。すなわち、「p・q」という関係なら、pqの両方とも真である場合しか、
2者の作る関係で真は出来ないので(真偽偽偽)という固有の値を作り、これが左の括弧の中身と
なる。(これらを掛け線の欄で表せばいわゆる”真理表”となる)ウィトゲンシュタインの写像理
論によれば、偽は事実と対応がないということを示すので、空欄のーで表すと(W---)となる。
また「p⊃q」も数理論理学では結果的に包含関係というより真理関係のみで理解されるようなも
のであったから、その真偽値のパターンの一つとして、(--W-)となり、また 同語反復命題、
トートロジーはどの場合も真になるので(WWWW)、逆に矛盾命題はどんな場合も偽となるので、
(----)となる。だから、所属する命題全てを否定する「N」は、(FFFW)もしくは(---W)
のパターンで表されるし、ξとなる要素命題が増えても、この全部否定する場合の真理値のパター
ンは必ず最後だけWとなる値を示すので、Nは一般に(---W)となる。
だから、
『 命題を項に持つ、括弧にくくられた表現ー括弧の中の各項の順序は問わないーを、私は
‘(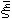 )’という記号で示すことにする。‘
)’という記号で示すことにする。‘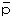 が、始めに与えられた(実際的にはわれわれの使用される命題から
要素命題の存在が要請されるといえるのだが)”すべての要素命題”を表すので(ラッセルの序文
より) それを素材として ”任意の幾つかの選ばれた命題” が
が、始めに与えられた(実際的にはわれわれの使用される命題から
要素命題の存在が要請されるといえるのだが)”すべての要素命題”を表すので(ラッセルの序文
より) それを素材として ”任意の幾つかの選ばれた命題” が 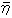 )とするならば〔
)とするならば〔