|
◆ p,17 ◆ |
|---|
|
【Kb・B】
『 限量記号は、独立変数の値のごとくあらわれる。 』（ TLP 5・523 ） と、云われるところは、端的に、ウィトゲンシュタインの全称記号、特称記号に関する考えが 顕れている。それは f（x）という表現や、f(a)という表現自体にもうすでにあるもの、とい う発想 といっていい。すなわち、先程触れた”命題の一般形式”とは、否定連言で結ばれた 関数表現された命題の一般形なのであり、その関数表現自体が限量記号の発想と重なっている ということになる。というのは、独立変数（x)は、それだけですべてのありうる全ての値を前 提にしており、また（a)なる値は、ある一つの値が存在するし、それがaであることを前提に している。 だから、 『 フレーゲとラッセルは、論理積ないし論理和と結びつけて、一般性を導入した。その 結果、命題‘（∃x）.fx’と‘（x).fx’が、一般性の観念と真理関数の観念をとも に内蔵していることは、理解しにくくなった。 』 （ TLP 5・521 ） フレーゲの場合なら、‘∀x’（全称）を基本記号として、‘∃x ’（特称）を、∀xと〜の複 合で表現するなどの、記号体系をつくる一方で、全称を連言の一般化として考えるが、そう考え れば連合がより基本的な記号となってしまうのであり、どういう関係が判らなくなってしまう。 だから、‘∀x’や‘∃x ’を用いた限量論理は、根本的に混濁した表現を持っており、したが ってウィトゲンシュタインは、便宜的役割しかそれらの記号を用いられないとする。（いわゆる、 ウィトゲンシュタインは、述語論理を認めないと 云われる問題。しかし、限量記号の含意要素 に難点があるということで、関数表現の中に存在するような”本来の述語論理”を当然認めた上 での議論となる。一方、フレーゲのような述語論理表現に慣れると確かに発想が形式論理学的な 概念中心の論理の見方の傾向が出てくる･･･不調和な分離の影響＆指標と命題の混乱････後述） 確かに、限量記号には、それが連言や選言と何となく、関連していそうな予感はするものなのだ が、結局、フレーゲやラッセルの体系では、その予感を無理なく体系の中で位置づけることが出 来ないのである。というのは、「すべての」とか「ある」というような概念は、すべての論理的 対象がどのようなしくみで、真-偽という、存在-非存在とつながっているか、すなわち根本的に 命題を成り立たせるものであるはずの真理関数の理論と関連して説明しなければならないのに、 少なくもフレーゲやラッセルではその肝心な部分が混濁していることとなる。 すなわち、ウィトゲンシュタインの場合、現実と言語が 物（対象）-事態-事実 と名辞-要素命 題-命題という単純な関係とされるので、（TLP 2 〜 2・0141などから･･）成立しうるすべて の命題の外形が、完全に定まってしまう。そこから、組み合わせられた命題と現実の対応、非対応 である真偽＝真理値による関数、すなわち真理関数のすべての場合の一般形が、単純に否定連言の みを使って |
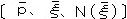と表現されうるなら、
「すべて」という概念も、その否定をくわえる一回前のかたち、
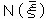＝〜（∃x）.fx の展開ではっきり規定できてしまうのである。（5・52）
一方、ラッセルやフレーゲの場合、言明における心理的な問題を排除できないし、クラス・タイプ
理論のように全体をいたずらに複雑化させる問題も絡むので到底 全体がどういうものか掴めない
のである。またラッセルの序文における、一般化の問題における難点の指摘として、与えられた命
題関数における”全ての命題”「限りある全体としての世界にいだく感情は神秘的なものだ」（TL
P 6・45 ）という部分を引用し、ウィトゲンシュタインが、ｘの値全体は神秘的で、語ることは
出来ないといっているとするのだが、これは曲解で、むしろウィトゲンシュタインの主張は、われ
われが、すべての とか一般的に というような言葉を使って話すとき、大体それに当てはまる言
明すべてを想定してしゃべっている、という程度の素直なモデル化に近く、そのイミでは神秘的で
も何でもない。（この”限りある全体”とは、”全体”と明らかに大きく違う意味で、ウィトゲン
シュタインはのべている。このことはTLP 6・4 以降の神秘や倫理について論じている問題と一
緒に考えたほうがいい。また、xの値の問題は、極限のなどの問題とも実は細かく云えばつながるの
だが、まずこういった考えの基本的方向を考えよう･･･）
ところで、否定連言の先程の”命題の一般形”は、どのようにして規定されているのか、過程を見
ていった場合、それが普通でない大変ややこしいやりかたで規定されていることは、本来もっと注
目されなければならなかったことだ。･･･